RSA [Cryptosystem]

Dear Readers,

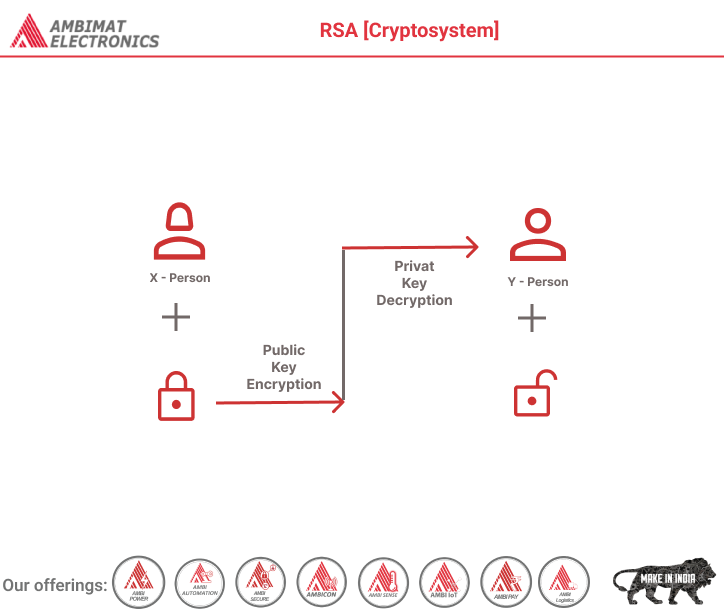
In this blog we are going to learn about, The RSA algorithm, a cornerstone of modern asymmetric cryptography, operates on the principles of using two distinct keys: a Public Key, which is shared openly, and a Private Key, which is closely guarded. In this asymmetric system, data can be encrypted with the Public Key and decrypted only by the corresponding Private Key, ensuring secure communication. RSA’s security foundation rests on the complexity of factoring large integers. The Public Key consists of two numbers, derived from the multiplication of two large prime numbers, while the Private Key is similarly derived from these primes. The difficulty of factoring these large numbers ensures the encryption’s strength. The RSA algorithm, typically employing 1024 or 2048-bit keys, remains robust against attacks, making it a fundamental tool for secure data transmission.

RSA algorithm is an asymmetric cryptography algorithm. Asymmetric actually means that it works on two different keys i.e. Public Key and Private Key. As the name describes that the Public Key is given to everyone and the Private key is kept private.

An example of asymmetric cryptography:

1. A client (for example browser) sends its public key to the server and requests some data.
2. The server encrypts the data using the client’s public key and sends the encrypted data.
3. The client receives this data and decrypts it.

Since this is asymmetric, nobody else except the browser can decrypt the data even if a third party has the public key of the browser.

The idea! The idea of RSA is based on the fact that it is difficult to factorize a large integer. The public key consists of two numbers where one number is a multiplication of two large prime numbers. And private key is also derived from the same two prime numbers. So if somebody can factorize the large number, the private key is compromised. Therefore encryption strength totally lies on the key size and if we double or triple the key size, the strength of encryption increases exponentially. RSA keys can be typically 1024 or 2048 bits long, but experts believe that 1024-bit keys could be broken in the near future. But till now it seems to be an infeasible task.

Let us learn the mechanism behind the RSA algorithm : >> Generating Public Key: 

Select two prime no's. Suppose P = 53 and Q = 59.
Now First part of the Public key  : n = P*Q = 3127.
 We also need a small exponent say e : 
But e Must be 
An integer.
Not be a factor of Φ(n). 
1 < e < Φ(n) [Φ(n) is discussed below], 
Let us now consider it to be equal to 3.
    Our Public Key is made of n and e

>> Generating Private Key: 

We need to calculate Φ(n) :
Such that Φ(n) = (P-1)(Q-1)     
      so,  Φ(n) = 3016
    Now calculate Private Key, d : 
d = (k*Φ(n) + 1) / e for some integer k
For k = 2, value of d is 2011.

Now we are ready with our – Public Key ( n = 3127 and e = 3) and Private Key(d = 2011) Now we will encrypt “HI”:

Convert letters to numbers : H  = 8 and I = 9
    Thus Encrypted Data c = (89e)mod n 
Thus our Encrypted Data comes out to be 1394

Now we will decrypt 1394 : 
    Decrypted Data = (cd)mod n
Thus our Encrypted Data comes out to be 89
8 = H and I = 9 i.e. "HI".

Below is the implementation of the RSA algorithm for

Method 1: Encrypting and decrypting small numeral values:

About Ambimat Electronics:

With design experience of close to 4 decades of excellence, world-class talent, and innovative breakthroughs, Ambimat Electronics is a single-stop solution enabler to Leading PSUs, private sector companies, and start-ups to deliver design capabilities and develop manufacturing capabilities in various industries and markets. AmbiIoT design services have helped develop Smartwatches, Smart homes, Medicals, Robotics, Retail, Pubs and brewery, Security.  

Ambimat Electronics has come a long way to become one of India’s leading IoT(Internet of things) product designers and manufacturers today. We present below some of our solutions that can be implemented and parameterized according to specific business needs. AmbiPay, AmbiPower, AmbiCon, AmbiSecure, AmbiSense, AmbiAutomation.

To know more about us or what Ambimat does, we invite you to follow us on LinkedIn or visit our website.

References:-

https://www.geeksforgeeks.org/rsa-algorithm-cryptography/