Dear Readers,
At the smallest scale in the computer, information is stored as bits and bytes. In this section, we’ll learn how bits and bytes encode information.
Bit
- a “bit” is atomic: the smallest unit of storage
- A bit stores just a 0 or 1
- “In the computer it’s all 0’s and 1’s” … bits
- Anything with two separate states can store 1 bit
- In a chip: electric charge = 0/1
- In a hard drive: spots of North/South magnetism = 0/1
- A bit is too small to be much use
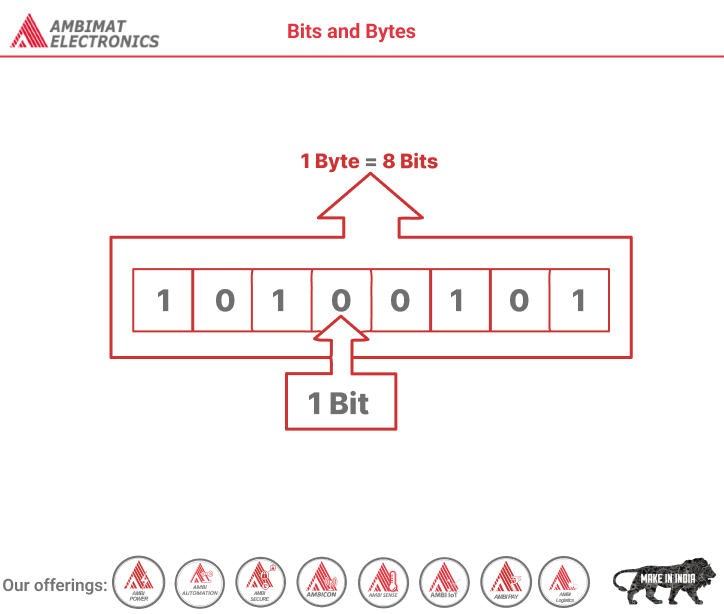
- Group 8 bits together to make 1 byte
Everything in a computer is 0’s and 1’s. The bit stores just a 0 or 1: it’s the smallest building block of storage.
Byte
- One byte = collection of 8 bits
- g. 0 1 0 1 1 0 1 0
- One byte can store one character, e.g. ‘A’ or ‘x’ or ‘$’
How Many Patterns With N Bits? (demo)
How many different patterns can be made with 1, 2, or 3 bits?
| Number of bits | Different Patterns |
| 1 | 0 1 |
| 2 | 00 01 10 11 |
| 3 | 000 001 010 011 100 101 110 111 |
- 3 bits vs. 2 bits
- Consider just the leftmost bit
- It can only be 0 or 1
- Leftmost bit is 0, then append 2-bit patterns
- Leftmost bit is 1, then append 2-bit patterns again
- 3-bits has twice as many patterns as 2-bits
| Number of bits | Different Patterns |
| 1 | 0 1 |
| 2 | 00 01 10 11 |
| 3 | 000 001 010 011 100 101 110 111 |
- In general: add 1 bit, double the number of patterns
- 1 bit – 2 patterns
- 2 bits – 4
- 3 bits – 8
- 4 bits – 16
- 5 bits – 32
- 6 bits – 64
- 7 bits – 128
- 8 bits – 256 – one byte
- Mathematically: n bits yields 2npatterns (2 to the nth power)
One Byte – 256 Patterns (demo)
- 1 byte is group of 8 bits
- 8 bits can make 256 different patterns
- How to use the 256 patterns?
- How to store a number in a byte?
- Start with 0, go up, one pattern per number, until run out of patterns
- 0, 1, 2, 3, 4, 5, … 254, 255
- One byte can hold a number between 0 and 255
- e. with 256 different patterns, we can store a number in the range 0..255
- Really good for storing characters/letters.
Bytes
- “Byte” – unit of information storage
- A document, an image, a movie .. how many bytes?
- 1 byte is enough to hold about 1 typed character, e.g. ‘b’ or ‘X’ or ‘$’
- All storage is measured in bytes, despite being very different hardware
- Kilobyte, KB, about 1 thousand bytes
- Megabyte, MB, about 1 million bytes
- Gigabyte, GB, about 1 billion bytes
- Terabyte, TB, about 1 trillion bytes (rare)
Bytes and Characters – ASCII Code
- ASCII is an encoding representing each typed character by a number
- Each number is stored in one byte (so the number is in 0..255)
- A is 65
- B is 66
- a is 96
- space is 32
- “Unicode” is an encoding for mandarin, greek, arabic, etc. languages, typically 2-bytes per “character”
| 32 space
33 ! 34 ” 35 # 36 $ 37 % 38 & 39 ‘ 40 ( 41 ) 42 * 43 + 44 , 45 – 46 . 47 / 48 0 49 1 50 2 51 3 52 4 53 5 54 6 55 7 56 8 57 9 58 : 59 ; 60 < 61 = 62 > 63 ? 64 @ |
65 A
66 B 67 C 68 D 69 E 70 F 71 G 72 H 73 I 74 J 75 K 76 L 77 M 78 N 79 O 80 P 81 Q 82 R 83 S 84 T 85 U 86 V 87 W 88 X 89 Y 90 Z 91 [ 92 \ 93 ] 94 ^ 95 _ 96 ` |
97 a
98 b 99 c 100 d 101 e 102 f 103 g 104 h 105 i 106 j 107 k 108 l 109 m 110 n 111 o 112 p 113 q 114 r 115 s 116 t 117 u 118 v 119 w 120 x 121 y 122 z 123 { 124 | 125 } 126 ~ |
Typing, Bytes, and You
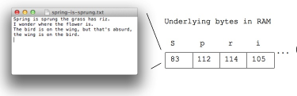
- Each letter is stored in a byte, as below
- 100 typed letters takes up 100 bytes
- When you send, say, a text message, the numbers are sent
- Text is quite compact, using few bytes, compared to images etc.
Numbers in Computers
- One byte works well for individual characters, but computers are also good at manipulating numbers.
- Integersare typically stored with either 4 or 8 bytes
4 bytes can store numbers between -2147483648 and 2147483647
8 bytes can store numbers between -9223372036854775808 and 9223372036854775807 - Adding in binary is just like normal addition with carrying
But when you run out of bits you can’t carry anymore
Leftmost bit indicates sign, so carrying to the leftmost bit changes a number ffrom positive to negative.
So adding 1 to 2147483647 goes to -2147483648!
Called Integer Overflow
Integer Overflow and Gangam Style
About Ambimat Electronics:
With design experience of close to 4 decades of excellence, world-class talent, and innovative breakthroughs, Ambimat Electronics is a single-stop solution enabler to Leading PSUs, private sector companies, and start-ups to deliver design capabilities and develop manufacturing capabilities in various industries and markets. AmbiIoT design services have helped develop Smartwatches, Smart homes, Medicals, Robotics, Retail, Pubs and brewery, Security.
Ambimat Electronics has come a long way to become one of India’s leading IoT(Internet of things) product designers and manufacturers today. We present below some of our solutions that can be implemented and parameterized according to specific business needs. AmbiPay, AmbiPower, AmbiCon, AmbiSecure, AmbiSense, AmbiAutomation.
To know more about us or what Ambimat does, we invite you to follow us on LinkedIn or visit our website.